The merits and weaknesses of Average Precision

When you are dealing with the evaluation of machine learning models, and in particular if you are working on object detection, you have come across the Average Precision metric. It is often thought of a quality assessment of a model that circumvents having to set a decision threshold, and is thus regarded as less prone to a choice of an important hyperparameter (the threshold) and thus a bit more objective.

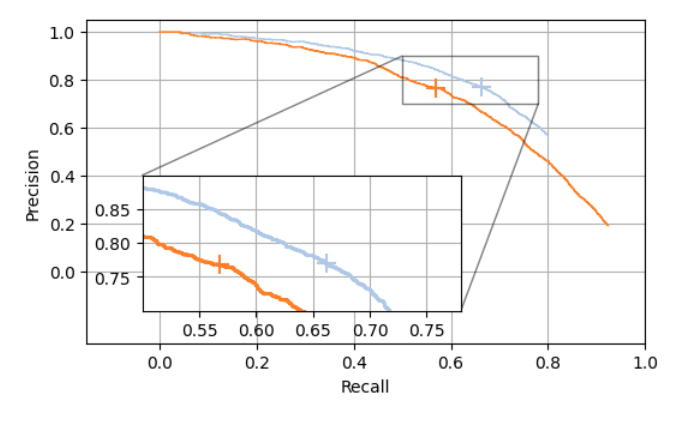
However, this is only part of the truth, as I will explain in this blog post. But let’s start in the beginning. The Average Precision tries to estimate the area under the precision recall curve. This is an example of such a curve from my experiments:

As you can see, it calculates several precision and recall values (depending on a variable decision threshold), and setting the threshold defines the operating point. It makes sense to not depend on a specific operating point, though for many applications a decision is ultimately necessary and defines the behavior of the model.

The core idea of the Average Precision is thus: Let’s just calculate the precision for a set of fixed recall values. However, as Hirling et al. point out in their very recent Nature Methods paper: There is not even a real consensus on how to calculate AP. In fact, they found five definitions in the literature.

But besides this: Let’s assume we have settled for a definition, e.g., the one used in the Pascal VOC metric. In this, they interpolate the precision value for each of the following 11 recall values: [0, 0.1, …, 0.9, 1.0]. So we can do this an approximate the area under the PR-curve with this.

Even then in many application domains not all precision and recall pairs are equally important.

The sensible area (of the PR curve)

In fact, for most applications, there is a sensible range for precision and recall values that could be viable, for example this area:

Too low recall values will be useless in practice, as well as too low precision values.

This practically restricts the area in which a sensible decision threshold should be set. This also means that a model can discard detections with very low confidence (reflecting the low precision) early on in the post-processing of the results. This is sensible, since the post-processing typically involves a non-maximum suppression (NMS), which compares each detection to each other and thus grows quadratically in terms of computational complexity with the number of detections. Getting rid of the low confident ones thus will speed up everything drastically, while not sacrificing detection performance in the sensible area.

But what happens for the precision values outside of the highest recall values? In all implementations that I have seen so far, it’s being extrapolated with the value 0.

An example comparing two models

If we compare the above two PR curves, we would clearly state, that the light blue model is considerably superior to the orange model. Yet, if we calculate the AP metrics for both, we find very similar values (the AP is 71 % for both). The reason for this is that the orange model reaches higher recall values (due to its lower detection threshold) than the light blue model (which uses a higher detection threshold). For a practical application, this makes the post-processing (and, in particular the non-maximum suppression) of the orange model slower, but, more severely: It just does not matter, since it’s outside the sensible area. No model with a precision of lower than 60% would be tolerated here.

The Average Precision can thus send us a wrong message.

What would be a remedy for this? I think that restricting the calculation of the Average Precision to sensible recall values (specific to the application) makes a lot of sense and recommend this to you (if you can define a sensible range).

If you are interested in reading more about misinterpretations of metrics, I recommend reading the following two papers:

Uncategorized